An inverse visualization for the elliptic law
March 2021Here are two nice facts on spectra of random matrices of large size .
When is a Girko matrix, the eigenvalues of asymptotically follow the circular law – they tend to be uniformly distributed in . By Girko matrix, I mean a matrix where all the entries are iid real[1] random variables, centered, with variance 1.
When is a Wigner matrix, the eigenvalues of asymptotically follow a semi-circle law, and in particular they are real. By Wigner matrix, I mean a symmetric matrix where all the entries on and above the diagonal are iid real random variables, centered, with variance 1.
What happens in between lies in the elliptic realm. If is a Wigner matrix, the symmetry of is indeed equivalent to being maximally correlated with its own transpose , since they are equal. One can thus create intermediary models between Girko and Wigner, by parametrizing the degree of correlation above and below the diagonal: for this, we just take to be a fully independent matrix (Girko), and set
The matrix is a Girko matrix; the matrix is a symmetric matrix and the matrix it is an antisymmetric matrix. In , the entries above and below the diagonal are correlated, in that if ,
It turns out that the eigenvalues of asymptotically follow the elliptic distribution: they tend to be uniformly distributed inside an ellipse, ie the domain defined by
The animated picture below is an illustration of this phenomenon, as seen from . 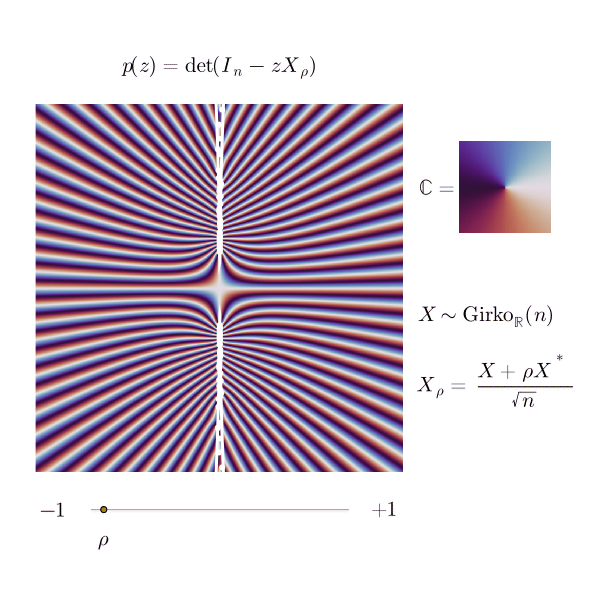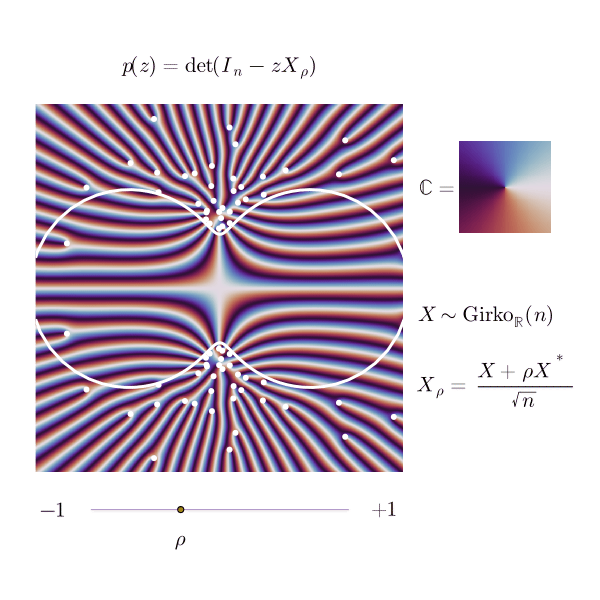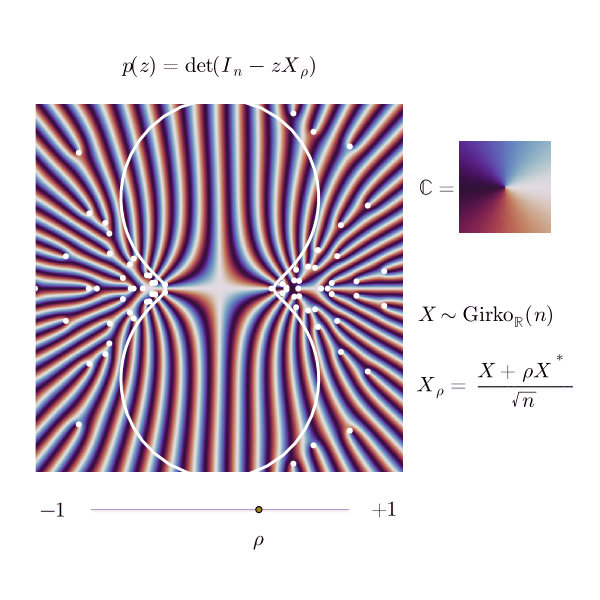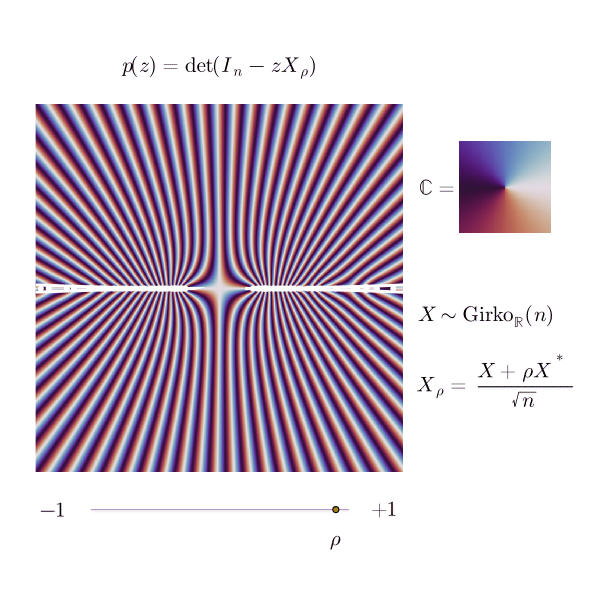
For several correlation parameters, I represented the phase portrait of the reciprocical of the characteristic determinant,
as a complex function; the white dots are the inverses of the eigenvalues of , and the white line is the inverse of the ellipse.
Polynomial convergence
The complex polynomial has degree . Its (complex) roots are the inverses of the (complex) eigenvalues of . The central picture in the preceding animation, with , illustrates a convergence phenomenon regarding , which recently appeared in a beautiful paper by Bordenave, Chafaï and García-Zelada.
They showed that if is a real Girko matrix entries centered and reduced, then
where are holomorphic functions; is deterministic,
while is itself a random function,
where the are iid standard real Gaussian random variables. The mode of convergence in (5) is the weak convergence of probability measures on the space – the space of holomorphic functions on the open unit disk, endowed with the classical topology of uniform convergence on compact sets.
Since the limiting random function does not vanish inside , one can use results like the Hurwitz theorem to show that when is large, it is highly unlikely that has a root inside – thus proving that the eigenvalue of with highest modulus, say , has with probability .
This is already visible in the picture corresponding to above, even though is pretty small here; the inverse eigenvalues seem to avoid the disk , or be very close to its boundary. Looking at the other pictures, one would merrily suppose that a similar statement holds for every between and , with no eigenvalue of being really far away outside of the ellipse boundary.
Notes and References
The original paper of Girko on the elliptic law... in Russian.
Convergence of the spectral radius of a random matrix through its characteristic polynomial, Bordenave, Chafaï, García-Zelada.
Comments on the circular law, a blogpost by Djalil Chafaï on open problems and recent works around the circular law.
My Julia code for the animated picture.
| [1] | I will stick to random matrices having real entries, but a similar picture holds with complex entries. |