Random line on the plane

August 2021

How do you draw lines at random in the plane, in such a way that the corresponding process does not depend on the origin?

Representing lines with points

Let $\ell$ be 2d line, ie a one-dimensional subspace of $\mathbb{R}^2$ .

Mathematically, it can be represented in many ways: for instance, if it is not vertical, there are two unique numbers $\alpha, \beta$ such that $\ell = \{ (x, \alpha x + \beta) : x \in \mathbb{R} \}$ . A less trivial way of representing lines is with orthogonality: if $\ell$ does not go through the origin, there is a unique couple $z=(r, \theta)$ with $r \geqslant 0$ and $\theta \in [0, 2\pi[$ such that $\ell$ is the unique line passing through the point $p=(r\cos(\theta), r\sin(\theta))$ , and orthogonal to the line $(0, p)$ . If $\ell$ passes through zero, the same is true provided that $\theta \in [0, \pi[$ .

This correspondance

\ell \leftrightarrow (\theta, r)

is one-to-one between the set of lines $\mathscr{L}$ , and the "strip" $\mathscr{A} = ]0, 2\pi [\times ]0, \infty [ \cup [0, \pi[\times \{0\}$ .

Random lines

A random line process is simply the set of lines obtained by sampling a random point process on the strip $\mathscr{A}$ and looking at the lines they represent.

For instance, a Poisson line process is nothing but the set of lines obtained by sampling a Poisson point process on $\mathscr{A}$ .

One could easily create many kinds of random processes by first sampling classical point process $\Phi$ in $\mathscr{A}$ , and then using the correspondance to get the line analog of this process. But...

Is it shift-invariant ?

Just as points in $\mathbb{R}^d$ , lines can be shifted. If $x$ is a point and $\ell$ a line, $\ell + x$ is simply the set $\{y+x : y \in \ell \}$ . A crucial question in geometric probability is to create random line processes $L$ that are shift-invariant: the distribution of $L$ , and the distribution of $L - x = \{\ell - x : \ell \in L \}$ must be the same.

While such a condition is not too difficult to check for many interesting point processes^[1], it is not so obvious for the kind of line processes I described above.

Indeed, when a line $\ell$ represented by $(\theta, r)$ is shifted by $x$ , its representation in $\mathscr{A}$ undergoes a non trivial transformation: if $\alpha$ is the argument of $x$ , then

\ell - x \quad \leftrightarrow \quad (\theta', |r'|)

where $r' = r + |x|\cos(\theta - \rho)$ , and $\theta' = \theta$ if $r>0$ , otherwise it is equal to $(\theta + \pi)$ modulo $2\pi$ .

Hence, if we note $T_x : \mathscr{A} \to \mathscr{A}$ the group of transformations described above, we obtain the simple caracterization: a line process is shift-invariant if its representation in $\mathscr{A}$ is $T_x$ -invariant for all $x$ . While this can be checked for what I described above as the Poisson line process, it also prevents other naive constructions from being stationary. For instance, sampling a Ginibre point process on $\mathbb{C}$ , then taking its restriction in the strip $\mathscr{A}$ does not yield a stationary line process.

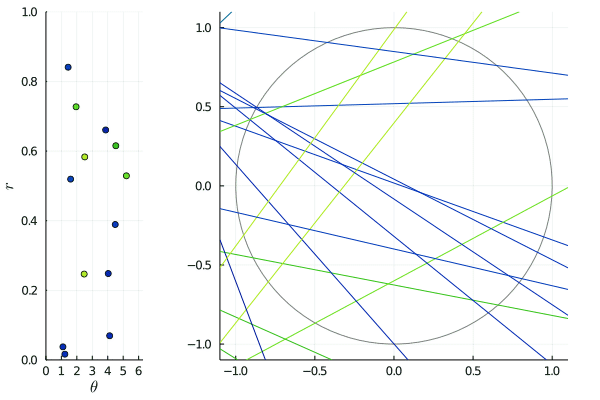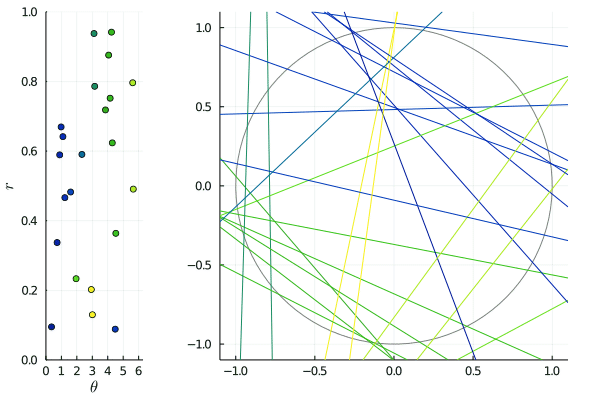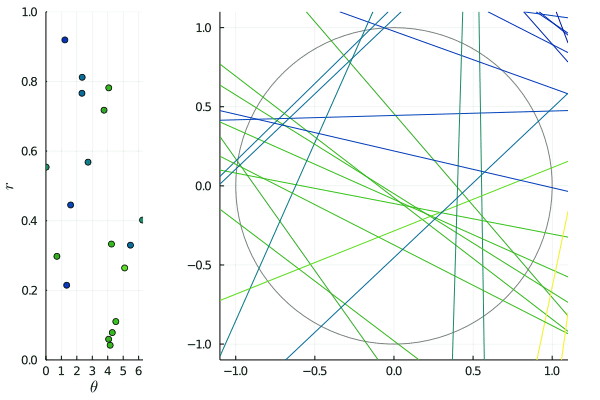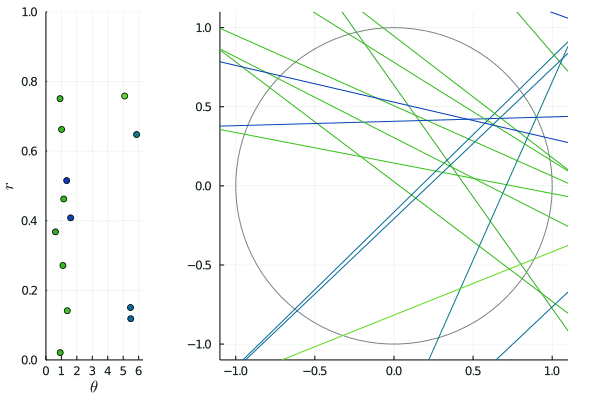
The animated picture shows the effect of such transformations: on the right, the lines are slowly shifted by $(t,0)$ for $t$ between $-2$ and $2$ , and on the left, we see the corresponding $\mathscr{A}$ -representation being transformed by $T_{(t,0)}$ . Since the shift is horizontal, horizontal lines merely move: this corresponds to the points on the lines $\theta = \pi/2, -\pi/2$ being invariant.

Is it isotropic ?

The same question can be asked with isotropy, that is: rotation invariance. When a line $\ell$ is represented by $(\theta, r)$ in $\mathscr{A}$ , rotating around the origin by an angle $\tau$ is the same thing as replacing $\theta$ by $\theta + \tau$ (modulo $2\pi$ ). Consequently, a line process is isotropic if and only if its representation in $\mathscr{A}$ is invariant with respect to the transformations $R_\tau : (\theta, r) \to (\theta + \tau, r)$ where the angle addition is taken modulo $2\pi$ .

A typical example of non-isotropic point process is obtained by choosing a finite set of directions, say $(\theta_1, \dotsc, \theta_k)$ , and for each of them to sample a translation-invariant point process $\Phi_j$ on $\mathbb{R}$ . The union

\{ (\theta_i, x) : i \in [k], x \in \Phi_i \}

is translation-invariant, but certainly not isotropic.

References

Stochastic geometry and its applications, by Chiu, Stoyan, Kendall and Mecke.
LineIntersections, some Julia code.