Random line on the plane
August 2021How do you draw lines at random in the plane, in such a way that the corresponding process does not depend on the origin?
Representing lines with points
Let be 2d line, ie a one-dimensional subspace of .
Mathematically, it can be represented in many ways: for instance, if it is not vertical, there are two unique numbers such that . A less trivial way of representing lines is with orthogonality: if does not go through the origin, there is a unique couple with and such that is the unique line passing through the point , and orthogonal to the line . If passes through zero, the same is true provided that .
This correspondance
is one-to-one between the set of lines , and the "strip" .
Random lines
A random line process is simply the set of lines obtained by sampling a random point process on the strip and looking at the lines they represent.
For instance, a Poisson line process is nothing but the set of lines obtained by sampling a Poisson point process on .
One could easily create many kinds of random processes by first sampling classical point process in , and then using the correspondance to get the line analog of this process. But...
Is it shift-invariant ?
Just as points in , lines can be shifted. If is a point and a line, is simply the set . A crucial question in geometric probability is to create random line processes that are shift-invariant: the distribution of , and the distribution of must be the same.
While such a condition is not too difficult to check for many interesting point processes[1], it is not so obvious for the kind of line processes I described above.
Indeed, when a line represented by is shifted by , its representation in undergoes a non trivial transformation: if is the argument of , then
where , and if , otherwise it is equal to modulo .
Hence, if we note the group of transformations described above, we obtain the simple caracterization: a line process is shift-invariant if its representation in is -invariant for all . While this can be checked for what I described above as the Poisson line process, it also prevents other naive constructions from being stationary. For instance, sampling a Ginibre point process on , then taking its restriction in the strip does not yield a stationary line process.
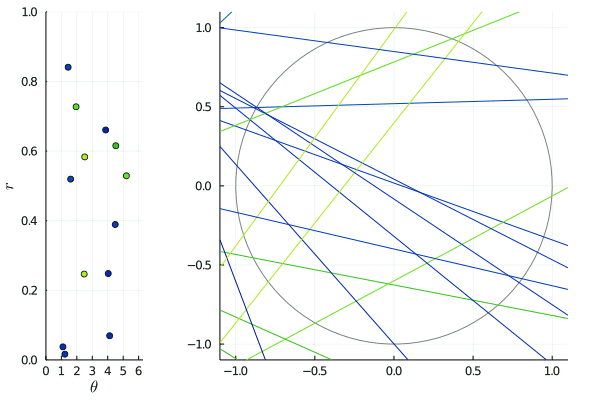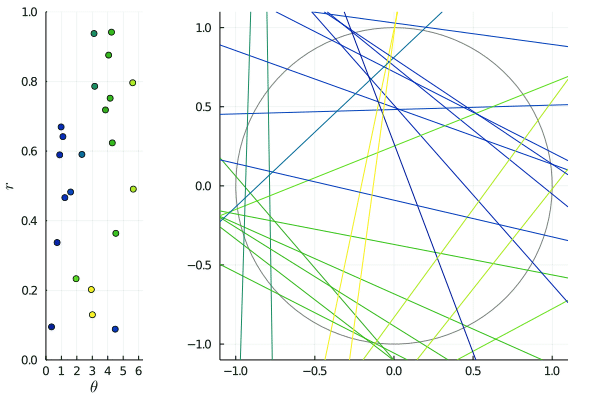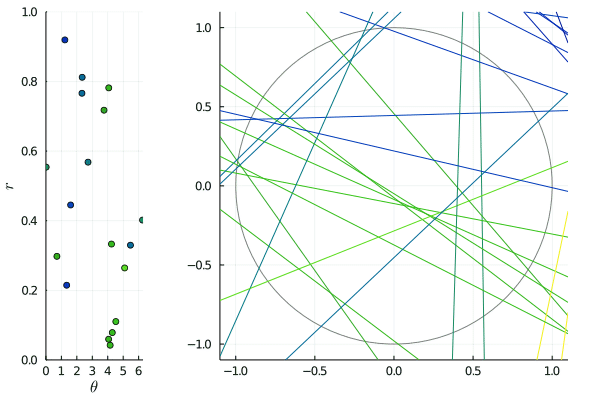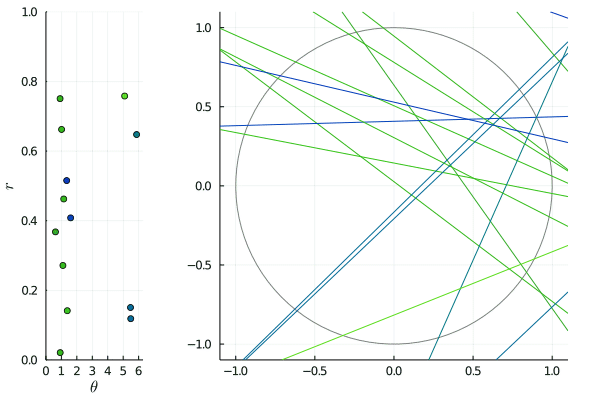
The animated picture shows the effect of such transformations: on the right, the lines are slowly shifted by for between and , and on the left, we see the corresponding -representation being transformed by . Since the shift is horizontal, horizontal lines merely move: this corresponds to the points on the lines being invariant.
Is it isotropic ?
The same question can be asked with isotropy, that is: rotation invariance. When a line is represented by in , rotating around the origin by an angle is the same thing as replacing by (modulo ). Consequently, a line process is isotropic if and only if its representation in is invariant with respect to the transformations where the angle addition is taken modulo .
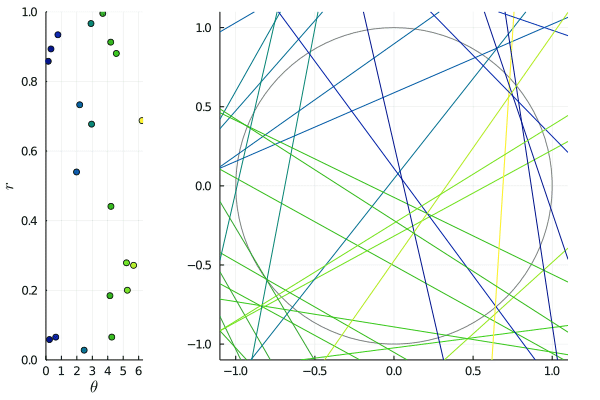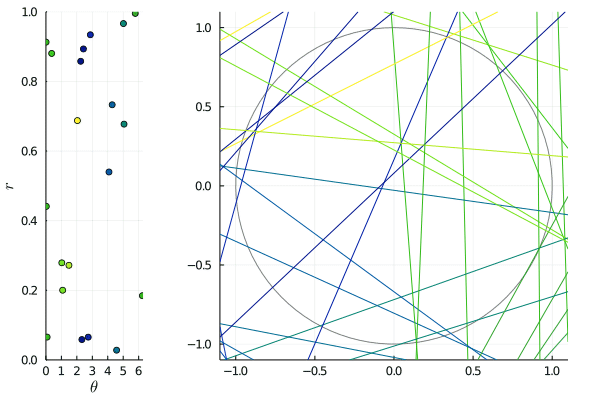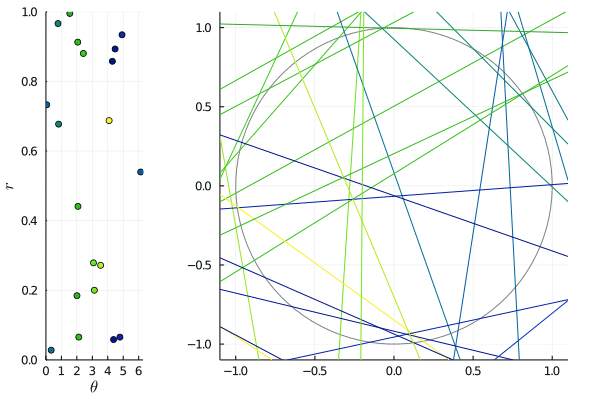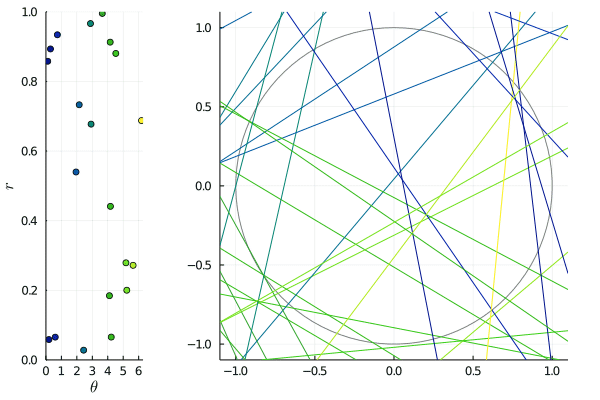
A typical example of non-isotropic point process is obtained by choosing a finite set of directions, say , and for each of them to sample a translation-invariant point process on . The union
is translation-invariant, but certainly not isotropic.
References
Stochastic geometry and its applications, by Chiu, Stoyan, Kendall and Mecke.
LineIntersections, some Julia code.
| [1] | for instance, for determinantal point processes it is trivially verified if the kernel itself is shift-invariant. |