Random analytic functions: Ryll-Nardzewski's theorem
April 2021In 1896, Émile Borel asked what can happen at the border of the disk of convergence of a Taylor series:
Étant donné une série de Taylor, il est intéressant de savoir si elle peut être prolongée en quelque manière au-delà de son cercle de convergence ou si ce cercle est une coupure.
This is a vast and difficult question, but surprisingly enough, it has an answer for random Taylor series, which are series whose coefficients are random.
At first sight, it might seem difficult to study the behaviour of a function which is itself random, and one might be tempted to say that random objects have random behaviours; but as Borel hinted in his 1896 paper, randomness comes with averaging, and averaging rules out eccentricity. That's the surprising result I would like to show in this note: this result essentially says that most random functions cannot be extended outside of their disk of convergence.
The precise statement is below; it is due to the Polish mathematician Czesław Ryll-Nardzewski in 1953.
Hadamard's formula
Let us remind a basic fact on the radius of convergence: if is a power series, its radius of convergence is given by Hadamard's formula,
Inside the disk , the power series converges, but this says nothing on what happens on the border of the disk or outside. Does approach a limit as approaches the border, for instance if ? Does it erratically diverge? Are there some points on the boudary, such that can be extended analytically around this point?
Think about the series . Its radius of convergence is 1, but since the sum is equal to , we can extend it at any point of the circle of radius 1, except at the point ; in fact, we can extend this function at every point of , even if the series representation only holds in the disk .
What happens at the border
We say that a complex number on the circle is regular if there is a such that can be extended analytically on . By the properties of analytic functions, this extension is unique. If a point is not regular, it is called singular.
The set of regular points of is an open subset of , and among functions with a radius of convergence equal to 1, it can have very different behaviours:
If , then the only non-regular point is , thus . Building on this example can construct functions with any finite number of singular points.
At the other side of the spectrum is . It can be shown using Hadamard's lacunary series theorem or any gap theorem that is empty, that is, there is no hope of extending on any open set containing some point in .
This last case where is empty might seem pathological; it is actually not. If is empty, we say that is a coupure for , following Borel's vocabulary.
Random analytic functions
In many of his works, Borel was interested in the behaviour of 'séries quelconques', as term he sometimes used to mean 'random'. A modern setting would be to take a sequence of (complex or real) random variables , and define
This is a random analytic function, and its radius of convergence is a random variable; however, classical theorems in probability such as Kolmogorov's zero-one law say that when the are independent[1], then is almost surely a constant – possibly .
Sometimes, this can be checked manually; this is the case for two common examples of random functions with a finite radius of convergence, the Rademacher and the Gaussian series.
Rademacher: is equal to or with probability . In this case for every , hence .
Gaussian: is a standard gaussian. In this case one can prove that too.
Look at the behaviour of (two realizations of) these functions, inside their radius of convergence.
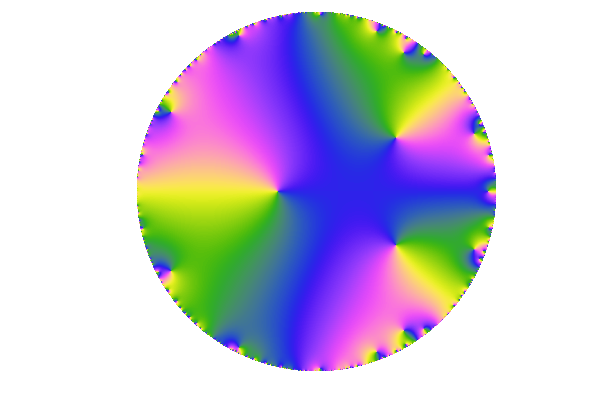
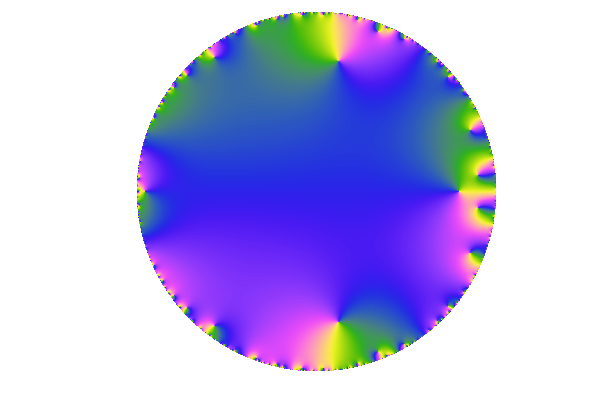
The Gaussian function is on top, the Rademacher function at the bottom. The small inset on the left is the color scheme for these domain colourings.
We can see a more and more erratic behaviour closer to the border of , with denser zeros and windings. It is tempting to say that both functions have a coupure at . That's actually the case and it's the content of the second part of this note.
Two theorems on random analytic functions
When is a random analytic function with a radius of convergence almost surely equal to 1, one can define as the set of all points which are almost surely regular for , and this set is an open set[2]. If it is empty, then has a coupure at .
Theorem
If the are symmetric random variables and if has a radius of convergence of , then either every point in is regular, or is a coupure for .
By symmetric, we mean that the law of and the law of are equal.
Proof. Let us suppose that is not empty. It contains a small arc interval of the circle, say , and there is an integer such that the arc length of this interval is bigger than . Now, if the are symmetric, then for any deterministic choice of signs , the law of the random analytic functions
are the same as the law of ; in particular, if we set to be if modulo and otherwise, we obtain a new random series with the same law as . But
for some function , which clearly satisfies . So, the left hand side of the preceding equation almost surely has as a regular set, hence so does the right-hand side. But since is invariant by rotations of angle , it means that the set of regular points of must also contain , which contains the whole circle ; in other words, can be extended outside , and so does .
We finally note that , so that . But this would mean that the set of regular points of contains .
In other words, either is empty, or it is equal to .
We now turn to the general case, where the distribution of the is not necessarily symmetric; with a clever argument, we can actually symmetrize them and use the preceding result to get Ryll-Nardzewski's theorem.
Ryll-Nardzewski's theorem
If the are random complex numbers such that almost surely has radius of convergence 1, then only two things can happen.
(1) Either the circle is a coupure of .
(2) Or, there is a deterministic analytic function with radius of convergence equal to 1, and such that:
the radius of convergence of is
the circle is a coupure for .
This was beforehand a conjecture, and it was proved by the Polish mathematician C. Ryll-Nardzewski; a few simpler proofs appeared afterwise. This one is notably simple and is drawn from J.-P. Kahane's book, Some random series of functions. The same statement actually holds on assumptions weaker than independence of the 's.
Proof. Let us suppose that we are not in the first case, that is, the set of almost sure regular points is not empty. We introduce another sequence of random variables , which are independent of the 's and have the same law. We note their Taylor series: it has the same distribution as .
Now, the coefficients of the random analytic function are , so they are symmetric and the preceding result applies: almost surely, has a coupure at its radius of convergence . Since both have radius of convergence 1, we must have : but can we have ? Well, since and both have a nonenmpty set of regular points on the circle of radius 1, it must mean that these points are also regular for : if has a coupure, it cannot be on the circle of radius 1, and we obtain .
Now comes the end: since and are independent, we can essentially consider that is not random... More precisely, conditionnaly on (almost every) realization of , the random function has a coupure at .
This last statement is actually much stronger than the statement of the theorem, since it means that there are many deterministic functions such that the conclusion holds: almost every realization of ...
The case
The last argument of the proof will be less shady if we allow an extra assumption: we can suppose that the are . Instead of considering one particular realization of , we can simply average with respect to , which has the same distribution as , so
The second case of the theorem now reads:
A Poisson example
I recently stumbled across an example illustrating this: consider the case where are independent Poisson random variables with parameter for some common . Routine arguments show that the radius of convergence of is , but in fact there is no coupure at . To see why, note that
so that
By elementary concentration arguments, it is possible to prove that , and consequently has a radius of convergence equal to , and the singularity at was really isolated. It is also possible to show that has a coupure at , thus giving a full illustration of Ryll-Nardzewski's theorem.
References
Jean-Pierre Kahane, Some random series of functions
Czesław Ryll-Nardzewski, D. Blackwell's conjecture on power series with random coefficients (Studia Math., 1953)
Émile Borel, Sur les séries de Taylor (C.R. de l'Acad., 1896)
Notes
| [1] | Note that we only asked the to be independent, not necessarily identically distributed. |
| [2] | The right way to define is as the union of all arc intervals with rationals, and such that almost surely every point in this interval is regular for . That way, is measurable (as a countable union of intervals) and every point in is almost surely regular. |