Flow models II: Score Matching Techniques

March 2025

The score of a probability density $p$ is the gradient of its log-density: $\nabla \log p(x)$ . This object is of paramount importance in many fields, like physics, statistics, and machine learning. In particular, it is needed if one wants to sample from the reverse SDE of a diffusion model. In this note, we survey the classical technique used for learning the score of a density from its samples: score matching.

Vanilla Score Matching
Tweedie's formula for denoising
Back to diffusions
Conclusion
References

Vanilla Score Matching

The Fisher Divergence

The L2-distance between the scores of two probability densities is often called the Fisher divergence:

\begin{aligned}\mathrm{fisher}(\rho_1 \mid \rho_2) &= \int \rho_1(x)|\nabla\log\rho_1(x) - \nabla\log\rho_2(x)|^2dx\\ &= \mathbb{E}_{X \sim \rho_1}[|\nabla\log\rho_1(X) - \nabla\log\rho_2(X)|^2]. \end{aligned}

Since our goal is to learn $\nabla\log p(x)$ , it is natural to choose a parametrized family of functions $s_\theta$ and to optimize $\theta$ so that the divergence

\int p(x)|\nabla\log p(x) - s_\theta(x)|^2dx

is as small as possible. However, this optimization problem is intractable, due to the presence of the explicit form of $p$ inside the integral. This is where Score Matching techniques come into play.

The score matching trick

Let $p$ be a smooth probability density function supported over $\mathbb{R}^d$ and let $X$ be a random variable with density $p$ . The following elementary identity is due to Hyvärinen, 2005.

Let

s : \mathbb{R}^d \to \mathbb{R}^d

be any smooth function with sufficiently fast decay at

\infty

, and

X \sim p

. Then,

\mathbb{E}[\vert \nabla \log p(X) - s(X)\vert^2] = c + \mathbb{E}\left[|s(X)|^2 + 2 \nabla \cdot s(X)\right]

where

c

is a constant not depending on

s

Proof. We start by expanding the square norm: $\begin{aligned}\int p(x)|\nabla \log p(x) - s(x)|^2 dx &= \int p(x)|\nabla \log p(x)|^2 dx + \int p(x)|s(x)|^2 dx - 2\int \nabla \log p(x)\cdot p(x)s(x) dx. \end{aligned}$ The first term does not depend on $s$ , it is our constant $c$ . For the last term, we use $\nabla \log p = \nabla p / p$ then we use the integration-by-parts formula:

2\int \nabla \log p(x)\cdot p(x)s(x) dx = 2\int \nabla p(x) \cdot s(x) dx = -2 \int p(x)( \nabla \cdot s(x))dx

and the identity is proved.

The loss we want to minimize is thus

\theta \in \argmin_\theta \mathbb{E}[\vert \nabla \log p(X) - s_{\theta}(X)\vert^2] = \argmin_\theta \mathbb{E}[|s_{\theta}(X)|^2 + 2 \nabla \cdot (s_{\theta}(X))].

Practically, learning the score of a density $p$ from samples $x^1, \dots, x^n$ is done by minimizing the empirical version of the right-hand side of (3):

\ell(\theta) = \frac{1}{n}\sum_{i=1}^n |s_{\theta}(x^i)|^2 + 2 \nabla \cdot (s_{\theta}(x^i)).

This looks computable… except it's not ideal. Suppose we perform a gradient descent on $\theta$ to find the optimal $\theta$ . Then at each gradient descent step, we need to evaluate $s_{\theta}$ as well as its divergence; and then compute the gradient in $\theta$ of the divergence in $x$ , in other words to compute $\nabla_\theta \nabla_x \cdot s_\theta$ . In high dimension, this can be too costly.

Denoising Score Matching

Fortunately, there is another way to perform score matching when $p_t$ is the distribution of a random variable corrupted with additive noise, as in our setting. The following result is due to Vincent, 2010.

Denoising Score Matching Objective

Let $s:\mathbb{R}^d \to \mathbb{R}^d$ be a smooth function. Let $X$ be a random variable with density $p$ , and let $\varepsilon$ be an independent random variable with density $g$ . We call $p_{\mathrm{noisy}}$ the distribution of $Y=X + \varepsilon$ . Then, $\mathbb{E}[\vert \nabla \log p_{\mathrm{noisy}}(Y) - s(Y)\vert^2] = c + \mathbb{E}[|\nabla \log g(\varepsilon) - s(Y)|^2]$ where $c$ is a constant not depending on $s$ .

Proof. Note that $p_{\mathrm{noisy}} = p * g$ . By expanding the square, we see that $\mathbb{E}[\vert \nabla \log p_{\mathrm{noisy}}(X+\varepsilon) - s(X+\varepsilon)\vert^2]$ is equal to

c + \int p_{\mathrm{noisy}}(x)|s(x)|^2dx -2\int \nabla p_{\mathrm{noisy}}(x)\cdot s(x)dx.

Now by definition, $p_{\mathrm{noisy}}(x) = \int p(y)g(x-y)dy$ , hence $\nabla p_{\mathrm{noisy}}(x) = \int p(y)\nabla g(x-y)dy$ , and the last term above is equal to $\begin{aligned} -2\int \int p(y)\nabla g(x-y)\cdot s(x)dxdy &= -2\int \int p(y)g(x-y)\nabla \log g(x-y)\cdot s(x)dydx\\ &= -2\mathbb{E}[\nabla \log g(\varepsilon)\cdot s(X + \varepsilon)]. \end{aligned}$ But then, upon adding and subtracting the term $\mathbb{E}[|\nabla \log g(\varepsilon)|^2]$ which does not depend on $s$ , we get another constant $c'$ such that

\mathbb{E}[\vert \nabla \log p_{\mathrm{noisy}}(X) - s(X)\vert^2] = c' + \mathbb{E}[|\nabla \log g(\varepsilon) - s(X + \varepsilon)|^2].

When $g$ is a centered Gaussian density, $\nabla \log g(\varepsilon) = (-\varepsilon / \mathrm{Var}(\varepsilon))g(\varepsilon)$ , hence everything is known in the formula, except for the $\mathbb{E}$ but this can be replaced by an empirical average over the training dataset.

Although this way of presenting score matching was popular in 2020-2022, it happens to be an avatar of a deeper, clearer result called Tweedie's formula. Although there is strictly nothing more in Tweedie's formula than in DNS, the presentation and derivation of the main formulas tells a richer story, and is now considered as a solid grounding for presenting score-matching techniques in diffusions.

Tweedie's formula for denoising

Herbert Robbins is often credited with the first discovery of Tweedie's formula in 1956 in the context of exponential (Poisson) distributions; a paper by Koichi Miyasawa (1961) was later rediscovered, with the first true appearance of the formula in a general, bayesian context. Miyazawa also computed second-order variants. Maurice Tweedie extended Robbin's formula, and Bradley Efron popularized it in his excellent paper on selection bias.

The link between Score, Hessian, and best denoiser

Tweedie's formulas

Let $X$ be a random variable on $\mathbb{R}^d$ with density $p$ , and let $\varepsilon$ be an independent random variable with distribution $N(0, \sigma^2 I_d)$ . We note $p_{\sigma}$ the distribution of $Y = X + \varepsilon$ . Then, $\begin{aligned} &\nabla \log p_\sigma(y) = - \mathbb{E}\left[\left. \frac{\varepsilon}{\sigma^2} \right| Y\right]\\ &\nabla^2 \log p_\sigma(y) = -\frac{I_d}{\sigma^2} + \mathrm{Cov}\left(\left. \frac{\varepsilon}{\sigma^2} \right| Y\right). \end{aligned}$ These expressions are equivalent to the noise prediction formulas, $\begin{aligned} &\mathbb{E}[\varepsilon \mid Y] = - \sigma^2 \nabla \log p_\sigma(Y)\\ &\mathrm{Cov}(\varepsilon \mid Y) = \sigma^2 I_d + \sigma^4 \nabla^2 \log p_\sigma(Y). \end{aligned}$ and to the data prediction or denoising formulas, $\begin{aligned} &\mathbb{E}[X \mid Y] = Y + \sigma^2 \nabla \ln p_{\sigma}(Y)\\ &\mathrm{Cov}(X \mid Y) = \sigma^2 I_d + \sigma^4 \nabla^2 \log p_\sigma(Y). \end{aligned}$

Finally, the optimal denoising error (the Minimum Mean Squared Error) is given by $\begin{aligned} \text{MMSE} &= \mathbb{E}[|X - \mathbb{E}[X \mid Y]|^2] \\ &= \mathrm{Tr}\left(\mathrm{Cov}(X \mid Y)\right) \\ &= \sigma^2 d + \sigma^4 \mathrm{Tr}\left(\nabla^2 \log p_\sigma(Y)\right). \end{aligned}$

The classical "Tweedie formula" is the first one in (14). The quantity $\mathbb{E}[X \mid Y]$ is the best guess of the original sample $X$ given its corrupted version $Y$ , hence the term "denoising formula".

Proof. We simply compute $\nabla \log p_\sigma$ and $\nabla^2\log p_\sigma$ by differentiating under the integral sign. Indeed,

\nabla \log p_\sigma(y) = \frac{\int \nabla_y \log p(x)g(y-x)dx}{p_\sigma(y)}.

Since $\nabla g(z) = -z/\sigma^2 g(z)$ , the expression above is equal to $-\int \frac{y-x}{\sigma^2} \frac{p(x)g(y-x)}{p_\sigma(y)}dx.$ The joint distribution of $(X, Y)$ is $p(x)g(y-x)$ and the conditional density of $X$ given $Y = y$ is $p(x|y) = p(x)g(y-x)/p_\sigma(y)$ , hence the expression above is equal to $-\mathbb{E}[\varepsilon/\sigma^2 \mid Y]$ as requested.

Now, by differentiating $\log p_\sigma$ twice, we get

\nabla^2 \log p_\sigma(y) = \frac{\int \nabla^2 p(x)g(y-x)dx}{p_\sigma(y)} - \left(\nabla \log p_\sigma(y)\right)\left(\nabla \log p_\sigma(y)\right)^\top.

Since $\nabla^2 g(z) = -(\sigma^{-2}I_d -\sigma^{-4}zz^\top )g(z)$ , we get

\nabla^2 \log p_\sigma(y) = -\frac{\int [\sigma^{-2} I_d- \sigma^{-4}(y-x)(y-x)^\top ] p(x)g(y-x)dx}{p_\sigma(y)} - \mathbb{E}\left[\frac{\varepsilon}{\sigma^2} \mid Y\right]\mathbb{E}\left[\frac{\varepsilon}{\sigma^2} \mid Y\right]^\top.

This is exactly $-\sigma^{-2}I_d + \sigma^{-4}\left(\mathbb{E}[\varepsilon\varepsilon^\top \mid Y] - \mathbb{E}[\varepsilon \mid Y]\mathbb{E}[\varepsilon \mid Y]^\top\right)$ , or $-\sigma^{-2}I_d + \mathrm{Cov}(\varepsilon / \sigma^2 \mid Y)$ .

The noise prediction formulas (13) directly follow from (12). For the denoising formulas, we only have to note that since $Y = X + \varepsilon$ , we have $\mathbb{E}[X \mid Y] = Y - \mathbb{E}[\varepsilon \mid Y]$ and $\mathrm{Cov}(X \mid Y) = \mathrm{Cov}(\varepsilon \mid Y)$ .

Since $Y$ is centered around $X$ , the classical ("frequentist") estimate for $X$ given $Y$ is $Y$ . Tweedie's formula corrects this estimate by adding a term accounting for the fact that $X$ is itself random: if $Y$ lands in a region where $X$ is unlikely to live in, then it is probable that the noise is responsible for this, and the estimate for $X$ needs to be adjusted.

Now, what's the link between this and Denoising Score Matching ? The conditional expectation of any $X$ given $Z$ minimizes the $L^2$ -distance, in the sense that $\mathbb{E}[X \mid Z] = f(Z)$ where $f$ minimizes $\mathbb{E}[|f(Z) - X|^2]$ . Formula (14) says that $\nabla \ln p_{\sigma}(y)$ , the quantity we need to estimate, is nothing but the « best denoiser » up to a scaling $-\sigma^2$ :

\nabla \ln p_{\sigma} \in \arg \min \mathbb{E}[|f(X + \varepsilon) - (-\varepsilon/\sigma^2)|^2].

I find this result to give some intuition on score matching and how to parametrize the network.

If $s(x)$ is « noise predictor » trained with the objective $\mathbb{E}[|s(X+\varepsilon) - \varepsilon|^2]$ , then $-s(x)/\sigma^2$ is a proxy for $\nabla \ln p_{\mathrm{noisy}}$ . This is called « noise prediction » training.
If $s(x)$ had rather been trained on a pure denoising objective $\mathbb{E}[|s(X+\varepsilon) - X|^2]$ , then $x - s(x)$ is a noise predictor for $X$ , hence $\sigma^{-2} (s(x) - x)$ is a proxy for $\nabla \ln p_{\mathrm{noisy}}$ . This is called « data prediction » training, or simply denoising training.

Both formulations are found in the litterature, as well as affine mixes of both.

Back to diffusions

Let us apply this to our diffusion setting where $p_t$ is the density of $\alpha_t X_0 + \varepsilon_t$ where $\varepsilon_t \sim \mathscr{N}(0,\bar{\sigma}_t^2)$ , hence in this case $g(x) = (2\pi\bar{\sigma}_t^2)^{-d/2}e^{-|x|^2 / 2\bar{\sigma}_t^2}$ and $\nabla \log g(x) = - x / \bar{\sigma}^2_t$ .

Data prediction model

The « data prediction » (or denoising) parametrization of the neural network would minimize the objective

\int_0^T w(t)\mathbb{E}[|s_{\theta}(t, X_t) - \alpha_t X_0|^2]dt.

This is the loss that was used to train most (but not all) diffusion models, up to the weighting $w$ . The SD1.5 and SDXL models use this formulation, hence if you have to use their U-NET you need to keep in mind that it's a denoiser. Here is the extract from the SDXL tech report:

Noise prediction model

Alternatively, the « noise prediction » parametrization of the neural network would minimize the objective

\int_0^T w(t)\mathbb{E}[|s_{\theta}(t, X_t) - \varepsilon|^2]dt

Up to the constants and the choice of the drift $\mu_t$ and variance $w_t$ , this is exactly the loss function (14) from the early DDPM paper: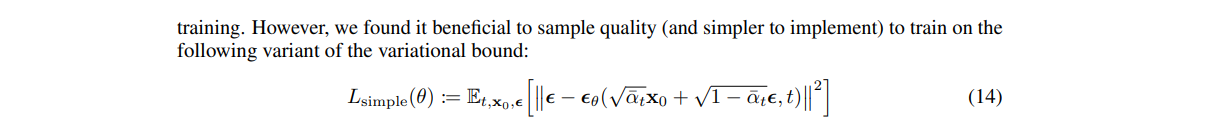

Sampling

Finally, one needs to plug these expressions back into the reverse SDE or ODE. If you want to play with pretrained models, you have to pay attention to how the model was trained: is it a data predictor or a denoiser? Based on the answer, one can go back to the score. Tweedie's formulas say that

\nabla \log p_\sigma(y) = \frac{\text{data predictor} - y}{\sigma^2}

while on the other hand

\nabla\log p_\sigma(y) = -\frac{\text{noise predictor}}{\sigma^2}.

Conclusion

We are now equipped with learning $\nabla \ln p_t$ when $p_t$ is the distribution of something like $\alpha_t X_0+\sigma_t \varepsilon$ . The diffusion models we presented earlier provide such distributions given the drift and diffusion coefficients, $\mu_t$ and $\sigma_t$ . But in general, we should be able to directly choose $\alpha$ and $\sigma$ without relying on the (intricate) maths behind the Fokker-Planck equation. This is where the flow matching formulation enters the game.

References

Hyvärinen's paper on Score Matching.

Efron's paper on Tweedie's formula - a gem in statistics.

I didnt find a free version of Miyazawa's paper, An empirical Bayes estimator of the mean of a normal population published in Bull. Inst. Internat. Statist., 38:181–188, 1961.